To solve Laplace’s equation in Java we are going to use the finite difference method. A very good explanation on how it is derived and the math behind it can be found online [1].
To start this process, we are going to create a pseudo 2D array in Java. This can be envisioned as discretizing our field into certain x-step and y-step elements (called Blocks in this code). To accomplish this, we will create an object called ValueBox where we cans store its value. Then we simply create a 2D array of the objects set to our desired size:
1
2
3
4
5
6
7
8
9
10
|
public class ValueBox {
public float value = 0f;
public boolean boundaryCondition = false;
public ValueBox(float value){
this.value = value;
}
}
|
1
|
private ValueBox[][] valueBoxArray = new valueBox[xBlocks][yBlocks];
|
Then we can set our boundary conditions for the system. For Dirichlet boundary conditions, the process is quite simple, we only need set the initial values (boundary conditions) of the boxes before we solve the iteration. We also need to flag the boxes as boundary conditions so that their value remains fixed. The following code snippet will set the bottom of the box, y = 0, to BC1 and the top of the box, y = yBlocks to BC2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
for(int x = 0; x < xBlocks; x++) {
for(int y = 0; y < yBlocks; y++) {
//Sets all blocks to an initial value
valueBoxArray[x][y] = new PathBox(0f);
//at y=0 boundary condition
if(y==0){
//sets it as a boundary condition
valueBoxArray[x][y].boundaryCondition = true;
//sets these blocks to boundary condition 1 (which can be any integer)
valueBoxArray[x][y].value = boundaryCondition1;
}
//at y = yBlocks boundary condition
if(y==yBlocks-1){
//sets it as a boundary condition
valueBoxArray[x][y].boundaryCondition = true;
//sets these blocks to boundary condition 2 (which can be any integer)
valueBoxArray[x][y].value = boundaryCondition2;
}
}
}
|
Now that we have are blocks initialized and boundary conditions set, here is the for general for-loop design that you will need to iterate over:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
for (int iteration = 0; iteration < 500; iteration++) {
for (int x = 0; x < xBlocks; x++) {
for (int y = 0; y < yBlocks; y++) {
//If the block is not a boundary condition
if (!valueBoxArray[x][y].boundaryCondtion) {
//If we are at the bottom row, but neither of the corners
if (y == 0 && x != 0 && x != yBlocks - 1) {
valueBoxArray[x][y].value = (0.3333f) * ((valueBoxArray[x + 1][y].value + valueBoxArray[x - 1][y].value + valueBoxArray[x][y + 1].value));
}
//If we are at the top row, but neither of the corners
else if (y == yBlocks - 1 && x != 0 && x != xBlocks - 1) {
valueBoxArray[x][y].value = (0.3333f) * ((valueBoxArray[x + 1][y].value + valueBoxArray[x - 1][y].value + valueBoxArray[x][y - 1].value));
}
//If we are at the right wall but at neither corners
else if (x == xBlocks - 1 && y != 0 && y != yBlocks - 1) {
valueBoxArray[x][y].value = (0.3333f) * ((valueBoxArray[x - 1][y].value + valueBoxArray[x][y - 1].value + valueBoxArray[x][y + 1].value));
}
//If we are at the left wall but at neither corners
else if (x == 0 && y != 0 && y != yBlocks - 1) {
valueBoxArray[x][y].value = (0.3333f) * ((valueBoxArray[x + 1][y].value + valueBoxArray[x][y - 1].value + valueBoxArray[x][y + 1].value));
}
//If we are at the origin
else if (x == 0 && y == 0) {
valueBoxArray[x][y].value = (0.5f) * (valueBoxArray[x + 1][y].value + valueBoxArray[x][y + 1].value);
}
//If we are at the bottom right corner
else if (x == xBlocks - 1 && y == 0) {
valueBoxArray[x][y].value = (0.5f) * (valueBoxArray[x - 1][y].value + valueBoxArray[x][y + 1].value);
}
//If we are at the top left corner
else if (x == 0 && y == yBlocks - 1) {
valueBoxArray[x][y].value = (0.5f) * (valueBoxArray[x + 1][y].value + valueBoxArray[x][y - 1].value);
}
//If we are at the top right corner
else if (x == xBlocks - 1 && y == yBlocks - 1) {
valueBoxArray[x][y].value = (0.5f) * (valueBoxArray[x - 1][y].value + valueBoxArray[x][y - 1].value);
}
//If we are anywhere in the middle
else {
valueBoxArray[x][y].value = (0.25f) * ((valueBoxArray[x + 1][y].value + valueBoxArray[x - 1][y].value + valueBoxArray[x][y - 1].value + valueBoxArray[x][y + 1].value));
}
}
}
}
}
}
|
Once the iterations are complete, you may simply print out the values or graph them from what is the valueBoxArray. 500 iterations is plenty, for smaller systems where the x-step and y-step elements are less than 100. However, if you are doing very large systems, >500 step elements, you may wish to check convergence by comparing the previous iteration value of a certain box after each loop.
Here are some examples of solutions where they are color coded based on value. Green = BC1 and Blue = BC2.
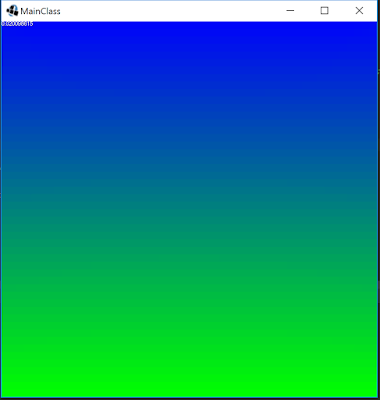 |
| At Y = 0, Value = BC1 and at Y = yBlocks, Value = BC2 |
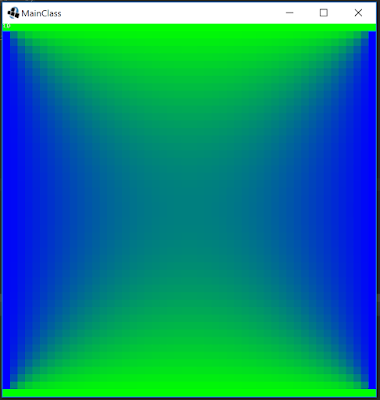 |
| At Y = 0 & Y = yBlocks, Value = BC1 and at X=0 & X=xBlocks, Value = BC2 |
Citations:
http://www.public.iastate.edu/~akmitra/aero361/design_web/Laplace.pdf